First published online.
It is the end of an era for education in the Eastern Cape as the man responsible for upskilling some of the province’s most influential mathematics and technical teachers hangs his hat on a career spanning more than four decades.
Dr Vasuthavan Govender, the chief education specialist at the Nelson Mandela Provincial Teacher Development Institute, is serving his last offi...
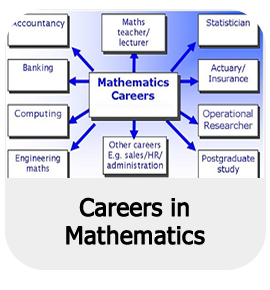
In September 2022, Grade 12 learner Benjamin Kleyn, from Parel Vallei High School in Somerset West in the Western Cape, triumphed over 134 university students in the annual South African Tertiary Mathematics Olympiad (SATMO), organised by the South African Mathematics Foundation (SAMF) and sponsored by Standard Bank.
...Mathematics is a critical skill in today's world, yet many parents struggle to help their children with their homework. The @Home with Mathematics project will bridge this gap by empowering parents and caregivers with the skills and knowledge they need to support their children's learning. With funding support, the South African Mathematics Foundation can continue to connect communities and create...
On 12 May every year, the mathematics community celebrates the International Day of Women in Mathematics. The day commemorates the birthday of the Iranian mathematician and Fields Medal recipient Maryam Mirzakhani (1977-2017). Maryam is a role model for female mathematicians worldwide. One such mathematician is Dr Cerene Rathilal, a lecturer at the University of KwaZulu - Natal’s School of Mathema...
In an effort to improve mathematics education in South Africa, the South African Mathematics Foundation (SAMF) is working in partnership with the African Institute for Mathematical Sciences’ Schools Enrichment Centre (AIMSSEC), to provide extensive teacher training to help improve the country’s mathematics outcomes.
...